Runnin ‘in the Rain’ : Does it matter whether you walk or dash? Japan prof. reveals truth

There’s a common belief that it doesn’t matter whether one walks or runs when caught in a downpour — the end result is you get equally drenched. Is that really the case? Using some grade-school math, professor Hiro Ito at the University of Electro-Communications in suburban Tokyo explains how that isn’t necessarily the case.
“It’s important to start by thinking in terms of the extremes,” Ito said. Comparing a 10-second run against an all-day walk over 100 meters in the rain, the run is the better choice when trying not to get wet. So, the aforementioned common theory can easily be debunked.
Assuming people are vertical lines:
Let’s take a look at a simple diagram to go a little further into the details. The first two diagrams depict the scenario of a 1-meter-tall person directly under rainfall coming straight down while aiming for a goal 100 meters away. In each, the blue vertical line on the left represents the person. The red boxes indicate the position of the rain which will strike the person along their path when the person is at the starting point.
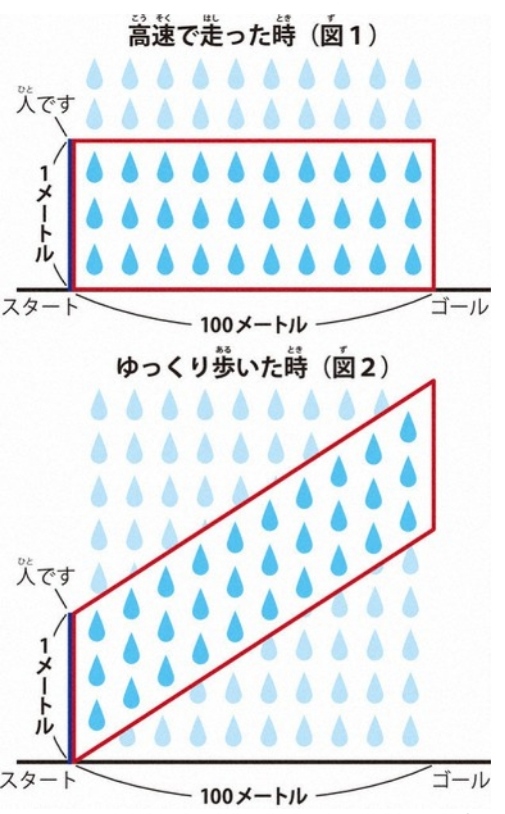
Diagrams 1 and 2 of Prof. Ito’s “Runnin’ in the Rain” formula. (Mainichi)
The box’s shape is rectangular if a person makes a dash from start to finish, as seen in diagram 1. On the other hand, the box is a parallelogram if the person walks slowly across the path, as seen in diagram 2. The slower the walk, the steeper the parallelogram’s angle, because the rain bound to fall on the person is higher up when they are at the starting point of their walk.
In either of the diagrams, the parallelogram’s dimensions are 1 m by 100 m, so the amount of rain within them is the same. However, since people are represented by lines here, these only show the amount of rain hitting a person’s front.
Taking people’s size into consideration
Since people are not lines, we have to add the following part to the equation. In diagrams 3 and 4, the person is represented by a blue-outlined rectangle of 0.5 m in width. In this case, we’ll also be able to look at how much rain hits the person’s upper side (the top of the rectangle).
In these diagrams, the pink box represents rain hitting a person’s front, while the shaded box above that represents how it hits the top of a person. In contrast to the pink box, the area of the shaded box differs depending on the angle from the ground. The more slowly someone walks, the more their upper body is hit with rain. With this in mind, we can conclude that the original hypothesis was incorrect.
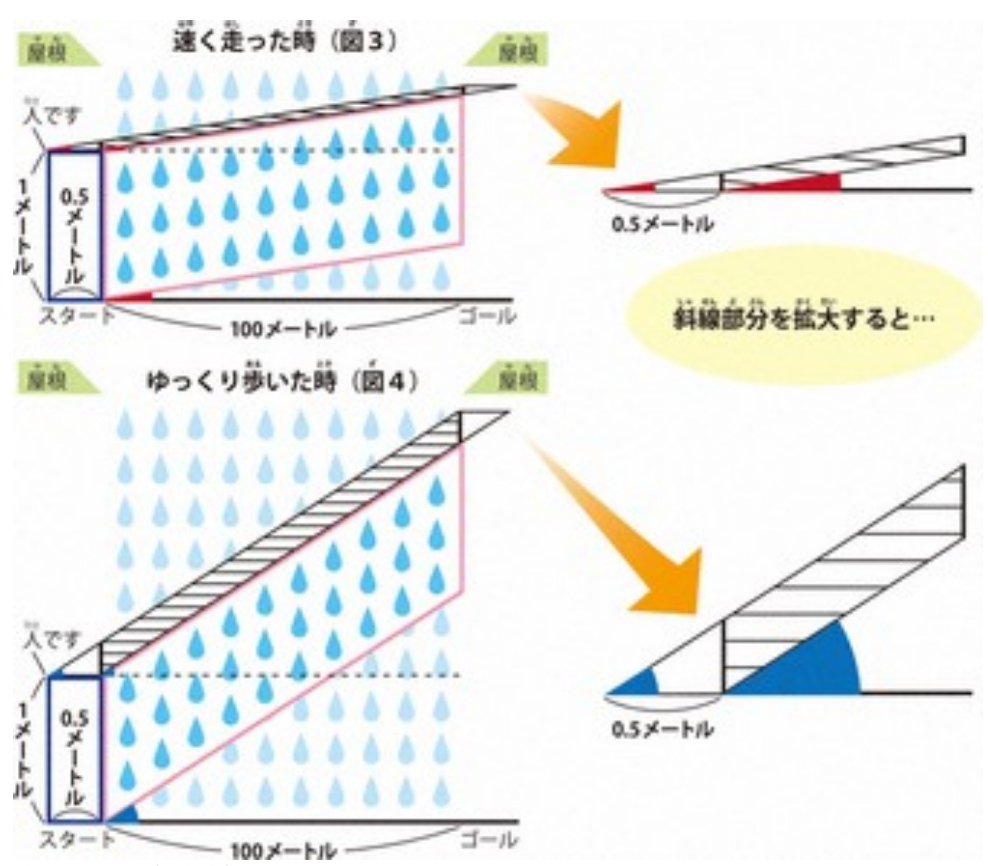
Diagrams 3 and 4. (Mainichi)
The “Runnin’ in the Rain Formula”
Now, using junior high and high school level mathematics, Ito offered us his “Runnin’ in the Rain Formula.” Supposing a person of 160 cm in height, 27 cm in breadth, a walking at a speed of 1.1 meters per second and a rate of rainfall of 7 m/s, the formula is as follows: RiR (x) = 0.5(1+1/x)
For example, when moving at twice the base walking speed, replace x with 2. This would equate to 0.75. In other words, the amount a person gets drenched is 75% that of the base speed scenario. With this formula, it becomes clear that no matter how quickly a person runs, they can only cut the wetness level by a maximum of 50% — even running at the speed of light.
Ito posted a detailed explanation of how he arrived at this formula, in Japanese, on his webpage http://www.alg.cei.uec.ac.jp/itohiro/columns2.html#column230620
For even the simplest of everyday problems, thinking mathematically can be extremely useful. “It’s very important to question whether something really is the way it is. The fun of math is being able to apply it to those questions,” Ito said.
Mainichi Japan




